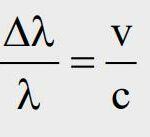Dans cet article, Axel GUILLERAND, rédacteur de ce dernier, a eu une idée : Serait il possible de mesurer la vitesse de rotation du Soleil avec son Sol’ex. Voici le récit de son cheminement.
Voici un article dont l’idée m’est venue à la suite d’un excellent post publié sur Astrosurf, que je résumerai ainsi : « Comment mesurer par spectrométrie le décalage de longueur d’onde du rémanent de supernova dénommé Nébuleuse du Crabe M1 par rapport à sa référence, et en déduire sa vitesse d’expansion immédiate».
Une comparaison était établie, dans cet article, entre les relevés photographiques effectués à quatorze ans d’écart, et la vitesse d’expansion de Messier 1 mesurée en une seule soirée par spectrométrie.
Je me suis alors posé les questions suivantes :
« Le raisonnement (que nous allons voir), qui y était tenu, était-il transposable à la vitesse de rotation du Soleil au moyen d’une mesure de ce que l’on appelle « l’effet Doppler » ? »
Deuxième question, un spectrohéliographe pour amateur de type Sol’ex était-il suffisamment précis pour cela ?
Troisième question, dans l’affirmative, quels seraient alors les outils informatiques à notre disposition ? A défaut, quels seraient les algorithmes à créer ?
I) La théorie
Supposons un spectrohéliographe de type « Sol’ex » créé on le sait par Christian Buil et Valérie Desnoux, et dont les caractéristiques sont les suivantes :
Fente d’entrée : 7 microns de large sur une longueur de 4,5 mm
Réseau orientable monté sur roue : 2400 traits/mm
Instrument d’acquisition 355 mm de focale et ouverture 60mm
Caméra d’acquisition : asi 178mm
Pour en savoir plus sur le Sol’ex, c’est ici et aussi ici.
Cet instrument est divisé en deux parties : fente/réseau, et réseau/caméra.
En résumé : la lumière, défocalisée après la fente en rayons parallèles, est réfléchie par le réseau, puis les rayons sont refocalisés avant d’être captés par la caméra.
L’ensemble est agencé avec un angle de 34 degrés, car lorsque le réseau mobile est orienté à 17 degrés, soit la moitié, il n’y a alors plus de dispersion spectrale, et nous sommes à ce qu’on appelle « l’ordre 0 ».
La caméra envoie enfin le signal échantillonné à l’ordinateur.
Les raies observées :
Les amateurs procèdent en pratique à des balayages dans la raie Hydrogène alpha, soit une longueur d’onde de 656,3 nanomètres, soit encore 6563 Angströms. Rappelons qu’un angström est égal à un dixième de nanomètre, lequel représente un millième de microns et donc un millionième de millimètre. Puis l’empilement nous permet d’améliorer la rapport signal/bruit.
La raie Hydrogène alpha est l’une des plus prisée des amateurs, celle dans laquelle l’électron unique a subi une altération du niveau 3 au niveau 2 autour du noyau1. C’est celle dans laquelle nous observons les filaments, protubérances, éjections, etc…
1: De n4 à n2, c’est le H beta, et de n5 à n2 le H gamma.
Sur le plan spectral cette raie présente, de manière plus significative que les autres, une déformation appelée « ailes » tirant soit vers le bleu, soit vers le rouge.
Cela s’explique par l’effet « Doppler-Fizeau » : tout objet en mouvement déplace la longueur d’onde de la raie spectrale par laquelle on l’observe. Cet effet est valable également dans les longueurs d’onde des fréquences sonores.
Remarquons également que sur le plan spectral, le fait que le Soleil soit en rotation sur lui-même explique que les raies du spectre soient cintrées et non rectilignes.
Une fois le balayage réalisé à l’aide de la monture équatoriale, on traite l’information avec le logiciel JSol’ex ou INTI, dans l’onglet « Doppler ». On obtient alors une image du Soleil avec un dégradé bleu dans la partie gauche, et rouge dans la partie droite. On peut paramétrer, en réglant le nombre de pixels à partir duquel cela générera un changement de couleur dans un sens ou dans l’autre. En clair, on peut régler l’intensité de l’effet bleu/rouge dans le logiciel de traitement.
Concrètement, le Soleil tourne de gauche à droite, d’est en ouest, et de notre point de vue dans l’hémisphère nord, la partie bleue (la gauche) vient vers nous tandis que la rouge (droite) s’éloigne de nous.
Voici un schéma résumant l’ensemble, vu au-dessus du Soleil et de la Terre :
On observe également que ce dégradé n’est pas uniforme, il peut y avoir des détails bleus dans le rouge et inversement. Il y a donc bien des micro variations de vitesse, dues à la nature plasmatique de l’objet observé et à la sismologie solaire. A l’inverse, si le Soleil était une boule de billard, tout serait parfaitement nuancé.
Tout ceci cependant n’est qu’une colorisation selon un seuil de décalage exprimé en pixel.
Mais cela ne nous dit pas la vitesse à laquelle le Soleil tourne-t-il sur lui-même !
II) Le problème
Il doit pourtant bien y avoir moyen d’appliquer la formule de Doppler Fizeau, laquelle s’exprime ainsi :
« La longueur d’onde observée, divisée par la longueur d’onde d’origine, multipliée par la constance de la vitesse de la lumière, nous donne la vitesse de déplacement de l’objet. »
Ou encore :« La longueur d’onde observée, divisée par la longueur d’onde d’origine, est égale à la vitesse de l’objet divisée par la constance de la vitesse de la lumière. »
Exemple dans l’article précité avec la nébuleuse du crabe, où c’est la raie OIII 4981,1 A, qui sert de repère :
Constat du décalage par rapport à la raie d’origine : +45 angströms
Application de la formule de Doppler Fizeau : v = 1350km/secondes !
Pour résoudre cette question, on serait tenté de mesurer la distance exprimée en pixels entre le centre de la raie H alpha et l’extrémité de ses fameuses ailes que j’ai mentionnées.
C’est ce décalage qui permettrait a priori de mesurer la vitesse à laquelle la rotation de l’astre influe sur la longueur d’onde dans laquelle nous l’observons.
On serait tenté aussi et pour cela d’utiliser dans un premier temps une image moyennée du scan de la raie H alpha, sur l’ensemble de la vidéo, ce qui va donc « lisser » les dentelures des ailes.
Image d’origine :
Image moyennée :
En réalité tout ceci se révèle très vite impossible :
1°) Où relever le pixel du centre de la raie ? Et où relever le pixel qui va nous indiquer la vitesse maximale révélatrice de l’accélération de notre astre sur lui-même, exprimée par rapport au centre de la raie de référence ?
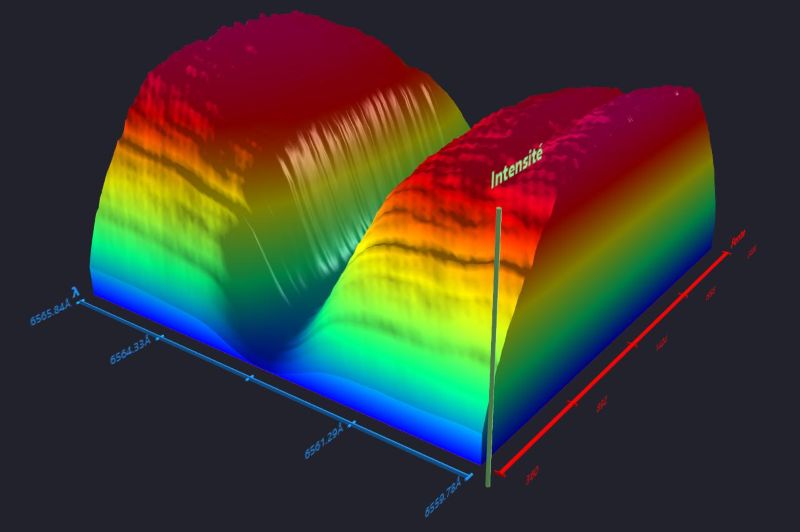
Même avec le profil de la raie en 3d, c’est inconcevable :
(Le centre de la raie est au plus profond du creux, le doppler au plus haut de la figure, au-delà c’est le continuum, c’est-à-dire l’absence de raie).
2°) Un réseau de 2400 traits nous offre dans notre configuration précitée une résolution déjà très élevée, égale à 40000 (il n’y a pas d’unités). Mais nous savons, sans dévoiler, que la vitesse du Soleil est d’environ 2kms par secondes, et à ce niveau cela supposerait que le Sol’ex offre une dispersion spectrale de 0,04 Angstroms par pixel. Or avec une résolution de 40000 la dispersion est dans notre cas de 0,063 A/p.
Note : La résolution (R) permet aussi de connaître la bande passante en divisant la longueur d’onde par R. Ici cela donne 6563/40000, soit 0,16 A, soit 0,016 Nanomètres.
A comparer avec la bande passante des filtre bloquants en visuel, soit entre 0,3 et 0,8 pour un Daystar Quark Chromosphère.
3°) La vitesse ne se mesure pas sur l’image de la raie elle-même, entre son centre et les ailes, mais sur le décalage du centre de la raie selon le point du Soleil où on l’observe. Cela signifie qu’il faut comparer la longueur d’onde en angströms du centre de la raie :
au centre du Soleil, d’une part,
et au niveau du limbe, d’autre part.
En effet à mi-chemin de son équateur, face à nous, le Soleil nous semble statique, alors son accélération maximale s’opère aux limbes.
On divisera ensuite le résultat de la formule de Doppler Fizeau par deux, puisque nous mesurons, et la vitesse bleue du limbe « est » au centre, et la vitesse rouge du centre au limbe « ouest », et non sur la totalité de l’objet.
4°) Qui plus est, le décalage de raie est infime, puisque la rotation du Soleil est bien moindre que l’expansion de M1 à 1350km/s.
5°) Enfin, la documentation sur Internet m’a semblé assez difficile pour un néophyte que je suis, même si je la mets en bibliographie. Je rappelle que je ne suis pas un scientifique…
J’ai donc posé la question suivante sur le Discord du logiciel JSol’ex, dont j’ai déjà parlé :
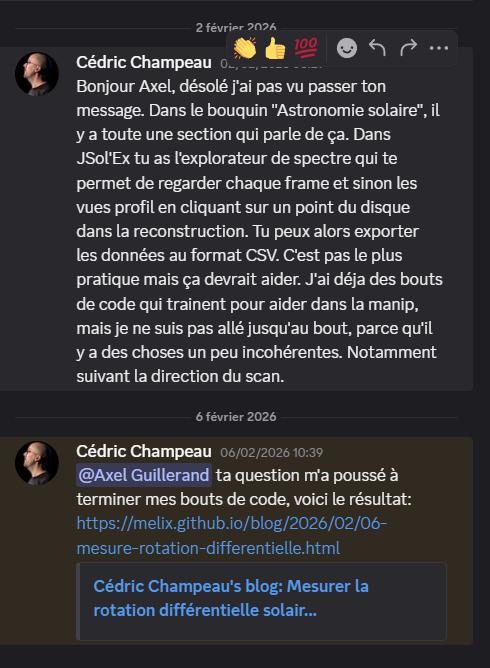
Ce à quoi Cédric Champeau, administrateur dudit Discord, créateur du logiciel, et que nous avions déjà rencontré aux Jason de 2025 avec Aurore, a répondu en quelques jours :
III) La solution
Cédric a désormais résolu ce problème dans la version 4.5.0 et en a fait un exposé complet dans son blog. C’est un énorme travail de codage, une fois de plus, et qui a permis de « forcer » les caractéristiques du spectrohéliographe.
Pour résumer la chose, sachant que le but du présent article n’est pas de vous noyer dans des détails :
Il faut abandonner les comparaisons de raies dédoublées comme par exemple dans le doublet du sodium Na D1 et D2, utilisées jusqu’à présent,
Il faut se focaliser sur les raies les plus fines et exploitables, ce qui exclut celles du calcium H et K, trop larges.
Il convient effectivement de tenir compte des différences de vitesse à l’équateur et aux pôles. Rappelons que cela est à l’origine de la rotation différentielle, elle-même cause de la dynamo solaire, et donc de la création des champs magnétiques, responsables des taches de la photosphère… qui elles-mêmes dans la chromosphère produiront des protubérances. On privilégiera donc obligatoirement de mesurer à l’équateur.
Il convient de tenir compte de l’angle P, exprimant la différence en degrés entre l’axe de rotation et le pôle solaire, puisque le Soleil est en effet incliné sur son axe, ce qui fausse nos observations opérées en ascension droite (d’est en ouest). Cet angle doit donc être annulé, par une « remise du Soleil d’aplomb », afin qu’à +90° nous soyons bien au pôle nord et non à un pôle nord + 3° par exemple. Sinon, cela fausserait la mesure à l’équateur.
Il faut trouver la position exacte du centre de la raie sur chaque image du scan, et il faut lisser le résultat au moyen de formules depuis longtemps éprouvées, que sont les profils de Voigt et de Lorentz.
IV) Le procédé
Ces obstacles franchis, et une fois la mise à jour vers la version 4.5.0 opérée, vous procéderez de la sorte :
Balayer le Soleil par le meilleur seeing possible, si possible en déclinaison plutôt qu’en ascension droite ;
Ouvrir JSol’ex 4.5.0.,
Lancer un traitement complet,
Un fois le traitement terminé, cliquer sur « analyse », puis « mesurer » (la vitesse différentielle).
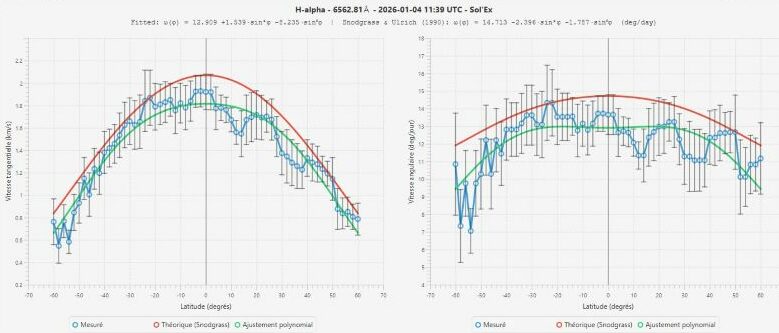
On obtient alors un graphique en deux parties, que j’ai ici généré à partir d’un scan dans la raie H alpha pris le 4 janvier 2026 à 11h39 utc :
On s’intéressera surtout au graphique de gauche, qui nous donne en ordonnées la vitesse sur toutes les latitudes du Soleil, lesquelles sont en abscisse.
La forme est en cloche, ce qui confirme la rotation différentielle.
On constate que la mesure précise à l’équateur donne bien 1,95 kms/s, ce qui est somme toute très précis pour un instrument amateur. En suivant la ligne verte du graphique on est plutôt à 1,8. Bien sûr, une résolution plus fine avec une fente moins large et un réseau plus dense donnera un résultat approchant encore plus celui donné par des instruments professionnels. Il faudrait aussi calculer sur plusieurs mesures, et en tirer une moyenne.
Avec votre Sol’ex et votre pc, vous pouvez alors désormais mesurer la vitesse de rotation du Soleil.
Cette nouvelle fonctionnalité, absolument formidable, offre donc un bel outil pour les enseignants, pour les clubs, … et pour les passionnés !
Repères Astro est une Association et Ecole d'Astronomie amateur de l'Oise dans les Hauts-de-France, à Vendeuil-Caply, entre Beauvais et Amiens. Nous avons une forte activité de vulgarisation scientifique auprès des scolaires et du grand public (Stages Etoiles, Animations, Nuits des Etoiles…), mais aussi une Section Photo active, un Planétariumtransportable, un Observatoire ainsi que de nombreux projets à venir. N'hésitez pas à prendre Contact avec nous.
Accueil EREA Joséphine Baker Crèvecoeur-le-grand Groupe 3 Repères accueille régulièrement des groupes d’élèves de l’EREA Joséphine Baker de Crèvecœur. Un partenariat qui dure depuis plusieurs [...]
